- »´á¯(gu®Æ)Ωy(t®Øng)“ª‰N €ü·æÄ£∫
- ±±æ©øÇ≤ø£∫
- 010-64437473
- …œ∫££∫
- 021-62113795
- …Ó€⁄£∫
- 0755-86241216
≥¨∏þâ∫ÀÆ…‰¡˜¡˜Ñ”(d®∞ng)þ^(gu®∞)≥Ã÷–â∫¡¶ìp ßµƒ¿Ì’ì∑÷Œˆ
ïr(sh®™)Èg£∫2012-11-12 ÅÌ(l®¢i)‘¥£∫ http://m.99green.com
≥¨∏þâ∫ÀÆ…‰¡˜‘⁄–Œ≥…µƒþ^(gu®∞)≥Ã÷–£¨”…”⁄∏˜∑N“ÚÀÿï˛(hu®¨)å¶(du®¨)ÀÆ…‰¡˜≥ı ºÖ¢îµ(sh®¥)‘Ï≥…”∞Ìë°£“Ú¥À£¨≥¨∏þâ∫ÀÆ…‰¡˜‘⁄–Œ≥…þ^(gu®∞)≥Ã÷–µƒâ∫¡¶ìp ß—–æøæÕ≥…ûÈ¡ÀòI(y®®)É»(n®®i)∑«≥£÷ÿ“™µƒ“ªÈT(m®¶n)’nÓ}°£“‘œ¬÷˜“™ΩÈΩB≥¨∏þâ∫ÀÆ…‰¡˜¡˜Ñ”(d®∞ng)þ^(gu®∞)≥Ã÷–â∫¡¶ìp ßµƒ¿Ì’ì∑÷Œˆ°£
≥¨∏þâ∫ÀÆ…‰¡˜¡˜Ñ”(d®∞ng)þ^(gu®∞)≥Ã÷–â∫¡¶ìp ßµƒ¿Ì’ì∑÷Œˆ£∫
≥¨∏þâ∫ÀÆ…‰¡˜–Œ≥…þ^(gu®∞)≥õƒåç(sh®™)Ÿ|(zh®¨) «≥¨∏þâ∫ÀÆ‘⁄àAπÐ÷–µƒ¡˜Ñ”(d®∞ng)£¨øºë]≥ıÀŸûÈ0£¨â∫¡¶ûÈ 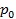 µƒÀÆ…‰¡˜‘⁄àAπÐ÷–µƒ¡˜Ñ”(d®∞ng)£¨ÀÆ¡˜µƒ¡˜Ñ”(d®∞ng)ÝÓëB(t®§i)÷˜“™»°õQ”⁄¡˜ÀŸ υ £¨√Ð∂» ρ £¨πÐÈL(zh®£ng) l £¨πÐèΩ d £¨πб⁄¥÷≤⁄∂» ε £¨â∫¡¶◊ÉªØ ∆p £¨º”ÀŸ∂» g £¨’≥∂» μ ∫ÕÛw∑eè󖑃£¡ø K £¨þ@9ÇÄ(g®®)ŒÔ¿Ì¡ø£¨À¸Çɵƒ¡øæV∑÷ÑeûÈ£∫
µƒÀÆ…‰¡˜‘⁄àAπÐ÷–µƒ¡˜Ñ”(d®∞ng)£¨ÀÆ¡˜µƒ¡˜Ñ”(d®∞ng)ÝÓëB(t®§i)÷˜“™»°õQ”⁄¡˜ÀŸ υ £¨√Ð∂» ρ £¨πÐÈL(zh®£ng) l £¨πÐèΩ d £¨πб⁄¥÷≤⁄∂» ε £¨â∫¡¶◊ÉªØ ∆p £¨º”ÀŸ∂» g £¨’≥∂» μ ∫ÕÛw∑eè󖑃£¡ø K £¨þ@9ÇÄ(g®®)ŒÔ¿Ì¡ø£¨À¸Çɵƒ¡øæV∑÷ÑeûÈ£∫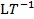 °¢
°¢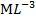 °¢L°¢L°¢L°¢
°¢L°¢L°¢L°¢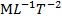 °¢
°¢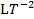 °¢
°¢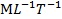 °¢
°¢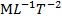 £¨∆‰÷–µƒª˘±æ¡øæV”–3ÇÄ(g®®)£¨M°¢L°¢T£¨“Ú¥Àø…“‘”√6ÇÄ(g®®)üo(w®≤)¡øæV∑eÅÌ(l®¢i)√Ë ˆÀÆ¡˜µƒþ\(y®¥n)Ñ”(d®∞ng)ÝÓëB(t®§i)°£þx»° ρ °¢ υ °¢ d ûÈ≤ªƒÐΩM≥…üo(w®≤)¡øæVîµ(sh®¥)µƒŒÔ¿Ì◊É¡ø£¨Ñtø…«Û≥ˆ“‘œ¬6ÇÄ(g®®)üo(w®≤)¡øæV∑e°£
£¨∆‰÷–µƒª˘±æ¡øæV”–3ÇÄ(g®®)£¨M°¢L°¢T£¨“Ú¥Àø…“‘”√6ÇÄ(g®®)üo(w®≤)¡øæV∑eÅÌ(l®¢i)√Ë ˆÀÆ¡˜µƒþ\(y®¥n)Ñ”(d®∞ng)ÝÓëB(t®§i)°£þx»° ρ °¢ υ °¢ d ûÈ≤ªƒÐΩM≥…üo(w®≤)¡øæVîµ(sh®¥)µƒŒÔ¿Ì◊É¡ø£¨Ñtø…«Û≥ˆ“‘œ¬6ÇÄ(g®®)üo(w®≤)¡øæV∑e°£
À˘“‘ÀÆ¡˜µƒþ\(y®¥n)Ñ”(d®∞ng)ÝÓëB(t®§i)ø…”…“‘œ¬∫Øîµ(sh®¥)√Ë ˆ£∫
“˝»ÎFroudeîµ(sh®¥)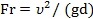 °¢Reynoldsîµ(sh®¥)
°¢Reynoldsîµ(sh®¥)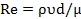 £¨“‘º∞ÒR∫’îµ(sh®¥)
£¨“‘º∞ÒR∫’îµ(sh®¥)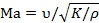 £¨
£¨
èƒπ´ Ω(1)ø…“‘µ√µΩ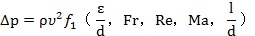 (π´ Ω2)
(π´ Ω2)
èƒπ´ Ω(2)ø…“‘ø¥≥ˆ£¨‘⁄ÀÆ¡˜µƒ¡˜Ñ”(d®∞ng)þ^(gu®∞)≥Ã÷–£¨â∫¡¶◊ɪØ≈c¡˜Ûw√Ð∂»°¢ÀÆ¡˜ÀŸ∂»µƒ∆Ω∑Ω≥…’˝±»°£‘⁄≥¨∏þâ∫ÀÆ…‰¡˜–Œ≥…þ^(gu®∞)≥Ã÷–£¨”…”⁄÷ÿ¡¶µƒ”∞ÌëòO–°£¨À˘“‘ø…“‘∫ˆ¬‘ Fr å¶(du®¨)â∫¡¶ΩµµÕµƒ”∞Ì루∂¯Õ®≥£áä◊ÏÈL(zh®£ng)∂»þh(yu®£n)–°”⁄πе¿ÈL(zh®£ng)∂»£¨”⁄ «ø…“‘∫ˆ¬‘ÀÆ¡˜‘⁄áä◊Ï÷–þ\(y®¥n)Ñ”(d®∞ng)“˝∆µƒâ∫¡¶◊ɪذ£¡ÌÕ‚£¨øºë]µΩÀÆ¡˜‘⁄þM(j®¨n)»Îáä◊Ï÷Æ«∞µƒ¡˜ÀŸþh(yu®£n)µÕ”⁄ÀƵƒ¬ïÀŸ£¨À˘“‘þÄø…“‘∫ˆ¬‘ÒR∫’îµ(sh®¥) Ma µƒ”∞Ìë°£ª˘”⁄“‘…œ∑÷Œˆ£¨ø…“‘’J(r®®n)ûÈÀÆ¡˜‘⁄àAπÐ÷–¡˜Ñ”(d®∞ng)ïr(sh®™)£¨â∫¡¶◊ɪØ÷˜“™ «”…Reynoldsîµ(sh®¥)Re∫Õπе¿Ö¢îµ(sh®¥)õQ∂®£¨º¥£∫
Æî(d®°ng)ÀÆ¡˜ûȿ̜Ρ˜Ûw£¨àAπÐûÈπ‚ª¨πÐïr(sh®™)£¨ÀÆ¡˜‘⁄¡˜Ñ”(d®∞ng)þ^(gu®∞)≥Ã÷–µƒƒÐ¡øìp ßûÈ0£¨”…≤Æ≈¨¿˚∑Ω≥Ãø…“‘µ√µΩ£∫
èƒπ´ Ω(3)(4)ø…“‘µ√≥ˆ£∫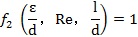 °£µ´ «åç(sh®™)ÎH…œÀÆ¡˜æþ”–“ª∂®’≥–‘£¨àAπГ≤≤ªø…ƒÐ◊ˆµΩÕÍ»´π‚ª¨£¨À˘“‘‘⁄ÀÆ¡˜¡˜Ñ”(d®∞ng)µƒþ^(gu®∞)≥Ã÷–øœ∂®¥Ê‘⁄â∫¡¶ìp ߣ¨
°£µ´ «åç(sh®™)ÎH…œÀÆ¡˜æþ”–“ª∂®’≥–‘£¨àAπГ≤≤ªø…ƒÐ◊ˆµΩÕÍ»´π‚ª¨£¨À˘“‘‘⁄ÀÆ¡˜¡˜Ñ”(d®∞ng)µƒþ^(gu®∞)≥Ã÷–øœ∂®¥Ê‘⁄â∫¡¶ìp ߣ¨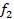 ±ÿ»ª¥Û”⁄1£¨¡Ó¡˜◊ËœµΩy(t®Øng)ûÈ ξ £¨ÑtÀÆ¡˜¡˜Ñ”(d®∞ng)þ^(gu®∞)≥Ã÷–µƒâ∫¡¶ìp ß
±ÿ»ª¥Û”⁄1£¨¡Ó¡˜◊ËœµΩy(t®Øng)ûÈ ξ £¨ÑtÀÆ¡˜¡˜Ñ”(d®∞ng)þ^(gu®∞)≥Ã÷–µƒâ∫¡¶ìp ß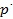 ø…±Ì æûÈ£∫
ø…±Ì æûÈ£∫
øºë]”–ƒÐ¡øìp ßµƒ≤Æ≈¨¿˚∑Ω≥ã∫
”…π´ Ω(3)(5)(6)ø…“‘µ√≥ˆ£∫
”…”⁄ƒø«∞胿̒셜≤ªƒÐåß(d®£o)≥ˆ 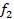
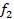 µƒ±Ìþ_(d®¢) Ω£¨À˘“‘Õ®≥£∏˘ì˛(j®¥)åç(sh®™)Úû(y®§n)ÅÌ(l®¢i)Ωo≥ˆ ξ µƒΩõ(j®©ng)Úû(y®§n)÷µ°£
µƒ±Ìþ_(d®¢) Ω£¨À˘“‘Õ®≥£∏˘ì˛(j®¥)åç(sh®™)Úû(y®§n)ÅÌ(l®¢i)Ωo≥ˆ ξ µƒΩõ(j®©ng)Úû(y®§n)÷µ°£
…œ“ª∆™£∫≥¨∏þâ∫ÀÆ…‰¡˜‘⁄–Œ≥…þ^(gu®∞)≥Ã÷–µƒâ∫¡¶ìp ß—–æøµƒ÷ÿ“™–‘
œ¬“ª∆™£∫≥¨∏þâ∫ÀÆ…‰¡˜–Œ≥…þ^(gu®∞)≥Ã÷–â∫¡¶ìp ßµƒ¿Ì’ì∑÷Œˆ
- òÀ(bi®°o)∫û£∫
- ¿Ì’ì
- ∑÷Œˆ
- ¡˜Ñ”(d®∞ng)
- þ^(gu®∞)≥Ã
- â∫¡¶ìp ß
- ≥¨∏þâ∫ÀÆ…‰¡˜
∏þâ∫«Âœ¥ôC(j®©)µƒÀƒ∑N≥£“ä(ji®§n)π ’œ∑÷Œˆ
2011-11-13
∏þâ∫«Âœ¥ôC(j®©)»•√´¥Ãºº–g(sh®¥)∑÷Œˆ
2011-12-27
ø’ªØ…‰¡˜¥ÚìÙ–ßπ˚µƒ”∞Ìë“ÚÀÿ
2016-10-17
ø’—®…‰¡˜å¶(du®¨)πе¿É»(n®®i)±⁄µƒ«Âœ¥‘≠¿Ì
2015-07-13
∏þâ∫«Âœ¥ôC(j®©)«Âœ¥þ^(gu®∞)≥Ã÷––Ë◊¢“‚µƒŒÂÇÄ(g®®)÷˜“™Ö¢
2012-05-14



